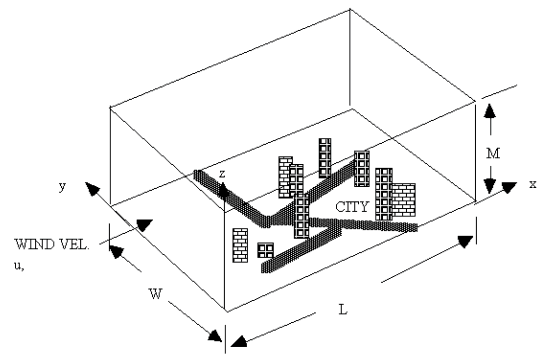
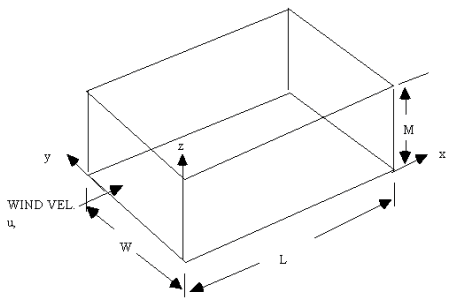
Consider a rectangular city with a rectangular plan.

Width = W
Length = L

And thus area = WL = A

Wind blows parallel to long side in direction x.

1) Atmospheric turbulence mixes pollutants completely up to mixing height M but above M no mixing takes place.

2) Turbulence in upwind direction is enough to give a uniform distribution within the "box".
I.e. there is no downwind trend in concentration. Clearly this is never completely true but it simplifies the mathematics.

3) Wind velocity u is constant and always in direction x. also untrue but again, it makes the mathematics "user friendly".
Here we use the average wind speed between ground level and M and for our purposes we could use the wind speed at half the height.

4) The concentration of pollution in air entering the "box" at x=0 is constant and equal to b (background concentration). Most models operate in µg/m³ but any suitable units are acceptable.

5) Air pollution emission rate Q is constant. This may also be given in terms of emission rate per unit area q.

q = Q/A.

Consider for yourself now the relationship between the units of q and Q and the units f the concentration we are measuring.

6) No pollutant enters or leaves through top of box nor through the sides parallel to wind direction.

7) The pollutant is conservative i.e. the destruction rate is zero within the time frame of the pollutant's life within the box.

Volume of system = WLM

Since all flows into and out of the box are constant we have a steady state and thus
"Accumulation rate = 0"

We consider the "emission rate " Q as a flow rate in from the lower face.

Thus

INWARD FLOWS?

There are two pollutant flows into the box:

Inward flow from upwind of the box = uWMb (units mass/unit time)

Inward flow from the lower face = Q = qWL

OUTWARD FLOWS?

Since we are at steady state the concentration in the 'box' is a constant c and the only outward flow is the flow out of the downwind face.

Flow out of the box = uWMc.

Thus

uWMb+qWL-uWMc = 0

uWMc=uWMb+qWL

uMc=uMb+qL

c = (uMb/uM)+(qL/uM)

c=b+(qL/uM)

Note that W does not enter the calculation but clearly the upwind concentration b is additive to concentration produced by city (for the long-lived pollutants we are considering). Concentration increases with q and L and decreases with u and M.

What does this tell us about the best design of a city for least pollution?