Diffusion Based Plume Models as Box Models

 

Despite the apparent dissimilarities between the fixed box model and diffusion models they can be considered to be closely related.

We could consider a situation as an imaginary box of pollutant that is moving along, downwind, at exactly the speed of the wind.
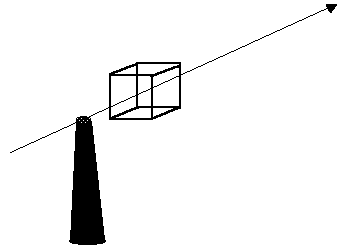If we start upwind of the stack the pollutant concentration is essentially zero but as we pass over the stack we pass into a region of high concentration. This high concentration is initially localised into a thin strand of pollutant but as the observer moves downstream we see the thread of contaminated air expands in the x and z direction. Imagine now the "box" is a small box near to the centre of the plume.
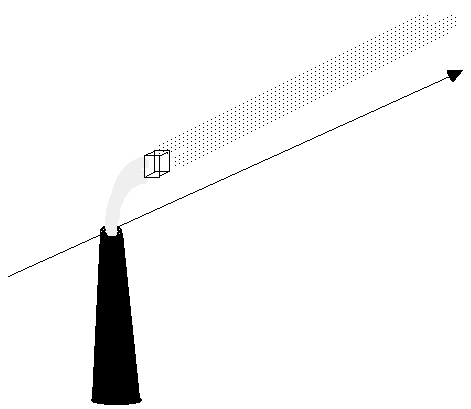If we assume the pollutant is conservative and none is generated in the plume.
Accumulation rate = sum of all flow rates in- sum of all flow rates out.
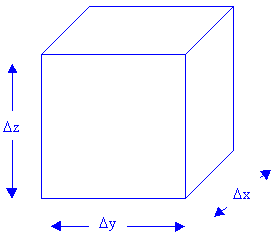The accumulation rate is the rate of change in the amount of pollutant the box contains and the amount the box contains is the product of concentration and volume.

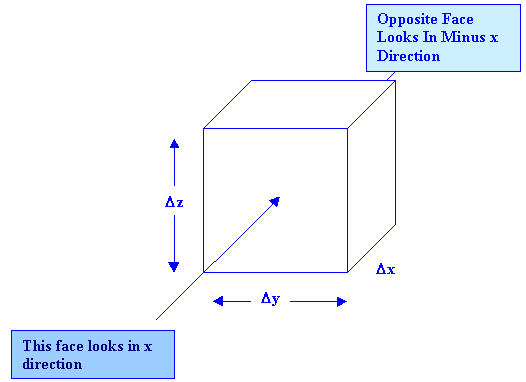
But since the box is moving at the speed of the wind there can be no bulk flow into the upwind face or out of the downwind face.

There is however movement in all three directions through turbulent mixing.

Diffusive plume models are based on these assumptions. We do not have a rigorous understanding of the mechanism of turbulent mixing but it can be estimated by saying that the flux of material being mixed across any surface is given by:

FLUX = RATE OF MASSFLOW PER UNIT AREA

c = CONCENTRATION

n = DISTANCE IN THE DIRECTION CONSIDERED(NORMALLY x,y,z)

K = TURBULENT DISPERSION COEFFICIENT.

Our cube has 6 faces of equal area
So we must rewrite our equation. We can develop this to show a relationship between concentration within the box and time. (And thus between concentration and distance downwind). We can eventually show that:

This equation is the basis of diffusion based models called K theory models.

The alternative approach to this diffusive system is based on looking at a random walk of individual pollutant "particles" under the influence of turbulence. This approach will not be considered further but suffice it to say that both the diffusive approach and the random walk approach result in essentially similar models.
We need to describe mathematically the following situation.
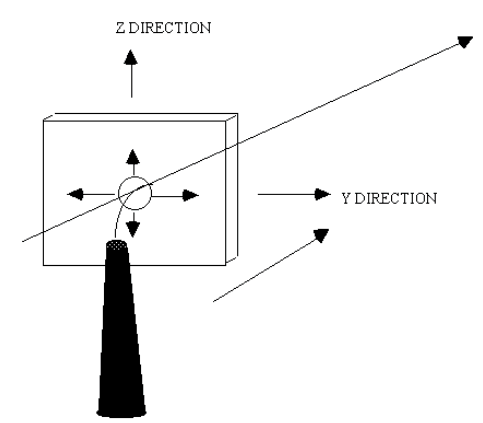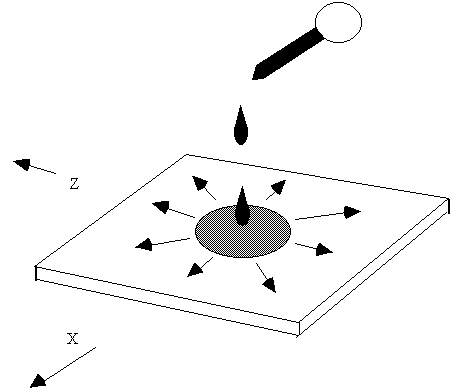
We can consider this, in the first instance as analogous to

Two dimensional spreading of a drop of ink in a thin "box" of water but we must remember that in reality turbulence serves to "stretch" the boundaries of the box, increasing concentration gradients and allowing "diffusion" to take place at a molecular level.

One version the Gaussian plume model does this by considering the slice as a series of small boxes with pollutant moving in and out of them with turbulence making the "diffusion rate" into some boxes faster than others.

What we need to do is solve for the concentration of the "dye" at any place and at any time from the application of the drop containing Xg of dye solution at a point z=0 and y=0.

If we do this we eventually get the equation:
Where the terms are related to the values of K in the "K Theory" equation above. This is often described as the basic Gaussian plume model. We expect that there will be more turbulent diffusion in the y direction than in the direction and that there will therefore be differences in the values of and . However before we consider this let us look at a very simple model and then at the concept of effective chimney height.