The Pursuit of Excellence
A Manager's Guide to Quality 		Specifications Revisited


Attempt 6

Finally, if we shift the average bearing radius down to 10.0mm, we will get the following distribution.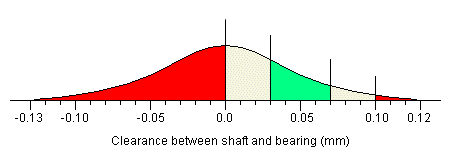

Distribution for average gap = 0.0mm

As you can see, the proportion of assemblies which will be too loose is very small, while the probability of finding that a randomly selected shaft will not fit a randomly selected bearing is much greater. Also, the proportion of assemblies that will fall into the 'ideal' range has been dropping ever since the average gap fell below 0.04mm, and it is now at its lowest level. The actual figures are as follows:

  • About 50% of the time, a randomly selected shaft and bearing will not fit together.

  • About 1% of the assemblies will be too loose.

  • About 19% of the assemblies will be ideal.

Using these percentages, we can construct a table to show what will happen at each level of assembly and reassembly.

Assemblies Don't Fit Total Accepted Ideal Too Loose
1000 500 500 190 10
500 250 250 95 5
250 125 125 48 3
125 63 62 24 1
63 32 31 12 1
32 16 16 6 0
16 8 8 3 0
8 4 4 2 0
4 2 2 1 0
2 1 1 0 0
1 0 1 0 0
2001 1001 1000 381 20

This means that of our 1000 assemblies, about 980 will be acceptable, and about 381 will be ideal.

The number of assemblies which are too loose (20), is clearly a great improvement on the 136 we got at the first attempt. However, the overall quality is clearly not as high, since the number of ideal units has dropped from a high of 434 to only 381. Also, what about the labour involved in getting these 980 working units? In order to produce our 1000 final assemblies, we will actually have to go through the process of assembling a shaft and bearing 2001 times.

Surely there must be a better way...