Attempt 2

The obvious solution to the problem presented in the previous attempt would be to try and reduce the number of unacceptable units by making the average gap narrower. So what happens if we reset the aim of the bearing process down by 0.01mm?

We are now producing bearings with a radius of 10.04mm ±0.09mm. This will mean that the distribution of the gaps will have moved down to 0.04mm ±0.13mm. The revised distribution is shown below.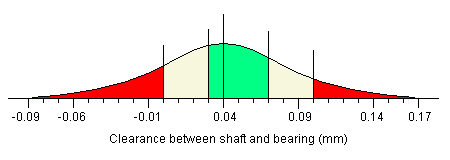

You will note that the red section at the right of the curve which shows the proportion of unusable assemblies has decreased, while the proportion of assemblies which will not fit has grown. By calculating the probabilities once again we find the following:

• About 17% of the time, a randomly selected shaft and bearing will not fit together.
  
  
• About 8% of the assemblies will be too loose.
  
  
• About 35% of the assemblies will be ideal.

This means that of our 1000 initial assemblies, about 170 won't fit, about 80 will be too loose, and about 350 will be ideal. Just as we did before, we shall have to refit the shafts and bearings which don't fit together. The table below shows what will happen at each level of assembly and reassembly.

In the end then, we will have gone through the process of assembling a shaft and a bearing together 1205 times to get 1000 final assemblies, of which 904 are suitable and only 422 are ideal.